diff options
Diffstat (limited to '')
| -rw-r--r-- | _posts/2023-04-20-chain-reactions-team.md | 101 |
1 files changed, 101 insertions, 0 deletions
diff --git a/_posts/2023-04-20-chain-reactions-team.md b/_posts/2023-04-20-chain-reactions-team.md new file mode 100644 index 0000000..dc7ac24 --- /dev/null +++ b/_posts/2023-04-20-chain-reactions-team.md @@ -0,0 +1,101 @@ +--- +title: Chain Reactions (Team) +categories: [Technical Logs, Team] +tags: [] +math: true +date: 2023-04-24 18:14:22 -0600 + +authors: [bryan, edgar] + +image: + path: https://upload.wikimedia.org/wikipedia/commons/thumb/1/1f/Depth-first-tree.svg/1200px-Depth-first-tree.svg.png + alt: "Depth First Search. Order in which the nodes are expanded. By: Alexander Drichel (https://commons.wikimedia.org/wiki/User:Alexander_Drichel)." +--- + +Try this problem by yourself first! Check the [Code Jam Page](https://codingcompetitions.withgoogle.com/codejam/round/0000000000876ff1/0000000000a45ef7). + +## Overview + +To find an approach for this problem, we had to analyze and take the important hints in the text to understand the problem and find a solution. + +The hints we found in the text and examples are: + +- Each module contains a fun factor. +- A module can point to other modules or the abyss. +- A chain ends when it reaches an already visited node or the abyss. +- The fun factor of an ended chain must be added to the total fun factor of the machines. +- An initiator module is the one that no other module points to it. +- All the chains must start at an initiator module. +- Given a chain we are going to take the max fun factor over the chain. +- If a chain ends, its max fun factor must be added up to the global fun factor of the machines. +- When different chains collide in a specific module, it is better to continue the chain with the smallest fun factor to make the global fun factor greater, because the smallest one can become greater in further modules. +- The modules can be represented as a forest. +- The abyss is the root of the forest. +- Each node that points to the abyss is the root node of a tree. + +As you can see in the following image, the machine can be represented as a tree. So, the trick to solve this problem is to handle it as a tree problem. + +The first thing to do is to find a way to start a chain from the initiator modules of the machine, which in this case are all the leaves in the tree. + +This could be done using the DFS Traversal through the tree. Using the DFS we are going to compare the fun factor of each node from the bottom of the tree. For each node in the tree, we are going to compare the fun factor of its children to choose the one that is going to continue the chain. + +To satisfy the condition of getting the global max fun factor in the forest, for each node in the forest, we are going to compare its children fun factor, and the smallest fun factor is the one that is going to continue the chain and the other children will be added up to the global fun factor. The child with the smallest fun factor is chosen, because it can become greater in further nodes, which means that the global fun factor can be greater at the end of the tree. + +In a nutshell... traverse the tree using DFS, for each node get the max fun fact of its children, choose the child with the smallest fun factor to continue the chain, and add up to the global fun factor the fun factor of each child that was rejected. + + + +<br> +<div style="text-align: center;">O O O</div> +<div style="text-align: center;">o o o</div> +<div style="text-align: center;">...</div> +<br> + +## Context + +Wile lives alone in the desert, so he entertains himself by building complicated machines that run on chain reactions. Each machine consists of $N$ modules indexed $1,\ 2,\ \ldots,\ N$. Each module may point at one other module with a lower index. If not, it points at the abyss. + +Modules that are not pointed at by any others are called initiators. Wile can manually trigger initiators. When a module is triggered, it triggers the module it is pointing at (if any) which in turn may trigger a third module (if it points at one), and so on, until the chain would hit the abyss or an already triggered module. This is called a chain reaction. + +Each of the $N$ modules has a fun factor $F_i$. The fun Wile gets from a chain reaction is the largest fun factor of all modules that triggered in that chain reaction. Wile is going to trigger each initiator module once, in some order. The overall fun Wile gets from the session is the sum of the fun he gets from each chain reaction. + +For example, suppose Wile has 4 modules with fun factors $F_1=60$, $F_2=20$, $F_3=40$, and $F_4=50$ and module 1 points at the abyss, modules 2 and 3 at module 1, and module 4 at module 2. There are two initiators (3 and 4) that Wile must trigger, in some order. + + + +As seen above, if Wile manually triggers module 4 first, modules 4, 2, and 1 will get triggered in the same chain reaction, for a fun of $\max(50,\ 20,\ 60)=60$. Then, when Wile triggers module 3, module 3 will get triggered alone (module 1 cannot get triggered again), for a fun of 40, and an overall fun for the session of $60+40=100$. + +However, if Wile manually triggers module 3 first, modules 3 and 1 will get triggered in the same chain reaction, for a fun of $\max(40,\ 60)=60$. Then, when Wile triggers module 4, modules 4 and 2 will get triggered in the same chain reaction, for a fun of $\max(50,\ 20)=50$, and an overall fun for the session of $60+50=110$. + +<br> +<div style="text-align: center;">O O O</div> +<div style="text-align: center;">o o o</div> +<div style="text-align: center;">...</div> +<br> + +## Solution + +As mentioned in the overview, the approach to get the solution of this problem was creating a forest, which is based on the inputs. Each tree in the forest (nodes that point to the abyss) is going to be traversed using the DFS traversal to get the initiators (leaves) of the tree. + +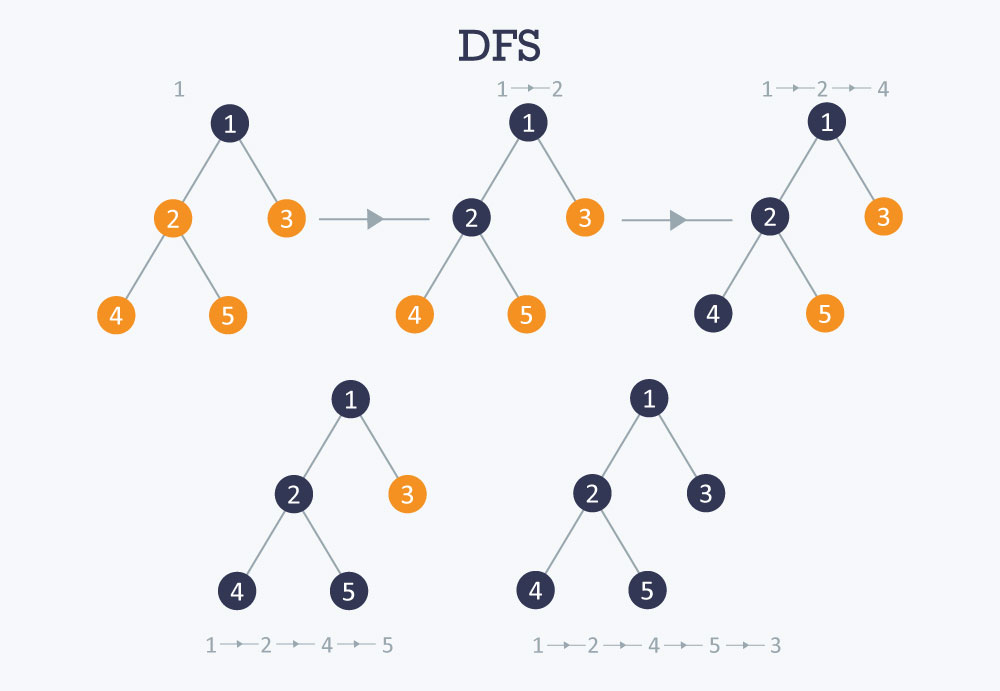 +_Depth First Search Implementation | Image Source - [HackerEarth](https://he-s3.s3.amazonaws.com/media/uploads/9fa1119.jpg)_ + +The DFS Is going to be useful to start the chains from the leaves of the tree. The trick to solve this problem is... for each root of a subtree select the child with the smallest fun factor, because that child is the one that will continue the path to the root of the tree. The other children become interrupted chains, so the fun factor of each interrupted child is going to be added up to the total max fun factor. + + + + +<br> +<div style="text-align: center;">O O O</div> +<div style="text-align: center;">o o o</div> +<div style="text-align: center;">...</div> +<br> + +## Alternative Solutions + +Another possible approach to this problem that avoids the use of recursion is by using a special `treeNode` class and a `flag` that indicates whether a node has children under it that must be processed first: + +1. If one of the children has sub nodes, then there are two ways to solve this problem, to leave the nodes intact, or to clear the useless data that is in the tree. +1. If one of the children of a child has children and we chose the first option we must have a flag that indicates the father that we don’t have to take the maximum calculated value of that branch and instead we have to analyze further, otherwise, the second option is to inherit the children of the child that we are analyzing only if my parent value is bigger than mine. + +Although the effect is similar, rather than just carrying a value from the leaf nodes up towards the root, we are also removing nodes that don’t contribute to the final solution from the "middle" of the tree, directly appending their child nodes to the parent node up a level. Resulting in the tree progressively shrinking. |
